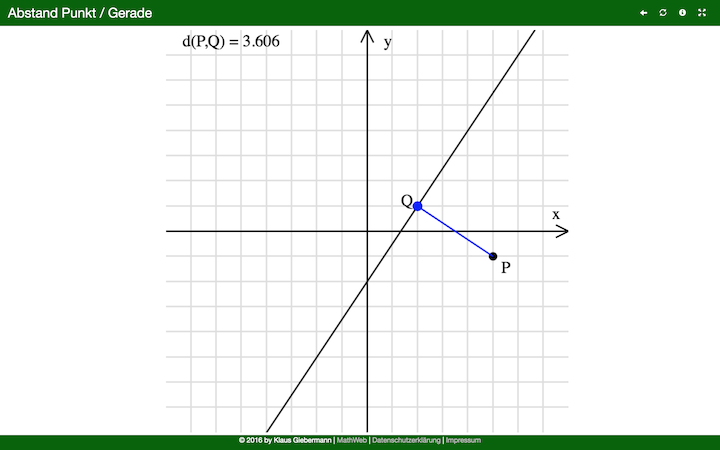
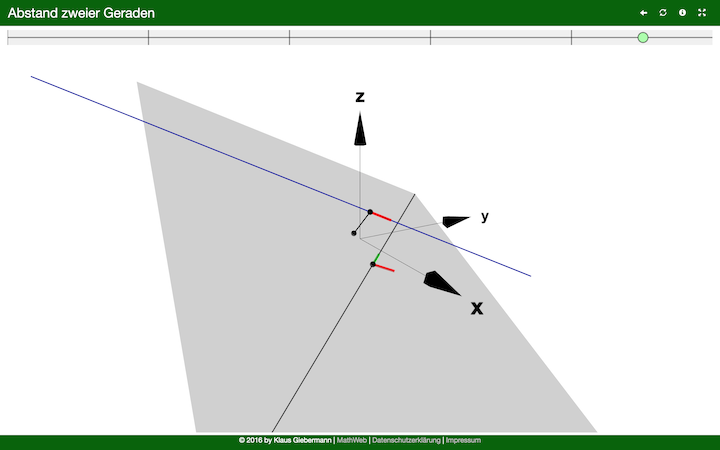
\[ g: \vec{x} = \left( \begin{array}{c} 1 \\ 2 \\ -2 \end{array} \right) + \lambda \left( \begin{array}{c} 2 \\ 1 \\ 1 \end{array} \right), \quad \lambda \in \mathbb{R} \]
Prof. Dr. Klaus Giebermann
Interaktive Demonstrationen
Interaktive Aufgaben
- Skalarprodukt und Vektorprodukt VektorproduktAusdruck mit Vektoren auswertenWinkel zwischen VektorenWinkel zwischen Vektoren (2)Fläche eines ParallelogrammsVolumen eines KörpersOberfläche eines KörpersWinkel zwischen VektorenOberfläche eines KörpersWinkel zwischen Vektoren (2a)Volumen eines TetraedersOberfläche eines TetraedersAusdruck mit Vektoren auswerten
- Darstellung von Geraden und Ebenen Parameterdarstellung einer GeradenParameterform einer EbenenKoordinatenform einer Ebene (1)Koordinatenform einer Ebene (2)Koordinatenform in Parameterform umwandelnHesse Normalform in Parameterform umwandelnParameterform in Koordinatenform umwandelnHesse-Normalform einer EbeneHesse Normalform in Parameterform umwandelnKoordinatenform in Parameterform umwandelnParameterdarstellung einer GeradenParameterform einer EbenenPunkt auf einer GeradenPunkt auf einer Geraden (2)Koordinatenform einer Ebene (3)Parameterdarstellung einer GeradenParameterform einer EbenenKoordinatenform einer Ebene (1)Koordinatenform einer Ebene (2)Koordinatenform in Parameterform umwandelnParameterdarstellung einer GeradenParameterform einer Ebenen
- Schnittprobleme Schnitt von zwei GeradenSchnitt von Gerade und Ebene (1)Schnitt von Gerade und Ebene (2)Schnitt von zwei Ebenen (1)Schnitt von zwei Ebenen (2)Schnitt von zwei Ebenen (3)Schnitt von zwei Ebenen (1)Schnitt von zwei Ebenen (2)Schnitt von zwei Ebenen (3)Abstand zum UrsprungSchnitt von zwei GeradenSchnitt von Gerade und Ebene (2)Schnitt von zwei Ebenen (1)